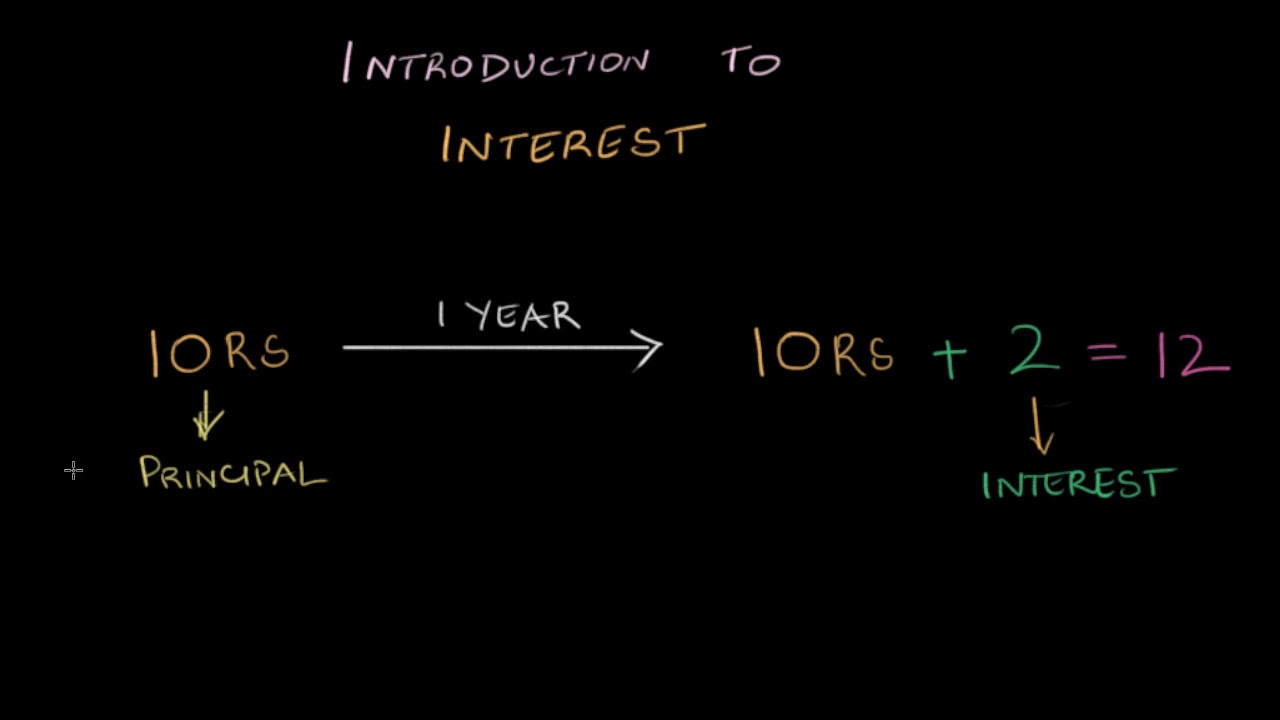
++ 50 ++ y=a(1+r)^t meaning 584976-Y=a(1+r)^t solve for r

The next function we look at is qnorm which is the inverse of pnorm The idea behind qnorm is that you give it a probability, and it returns the number whose cumulative distribution matches the probability For example, if you have a normally distributed random variable with mean zero and standard deviation one, then if you give the function a probability it returns the associated ZscoreExponential Growth = 100 * (1 10%) ^36;A function of the form y = a(1 r)t, where a > 0 and r > 0, is an exponential growth function initial amount time growth factor rate of growth (in decimal form) final amount y = a(1 r)t WWhat You Will Learnhat You Will Learn Use and identify exponential growth and decay functions Interpret and rewrite exponential growth and decay functions

Exponential Functions Mathbitsnotebook A1 Ccss Math

Y=a(1+r)^t solve for r

Y=a(1+r)^t solve for r-> ttest(x,y) Welch Two Sample ttest data x and y t = , df = , pvalue = 042 alternative hypothesis true difference in means is not equal to 0 95 percent confidence interval sample estimates mean of x mean of y > ttest(x,y,varequal=TRUE) Two Sample ttest data x and y t =Internal data from LandWatch records $1 billion of farms, ranches and other land listings for sale in New Hampshire With thousands of properties and rural land for sale in the state, this covers a combined 37,130 acres of land for sale in New Hampshire

Intro To Simple Interest Video Khan Academy

Baran Lab T h e C h e m i s t r y o f 1A c y l p y r i d i n i u m s D W Lin 5 This strategy can also be applied to the 1,2addition of enolates to define two asymmetric centers with antistereochemistry NWe can think of acceleration as "pulling" the velocity vector in a certain direction At t =1, the velocity vector points down and to the left;106 Exponential Growth and Decay Exponential decay equation #1 – y = a (1 – r) t y = what's leftover a = what you start with r = rate t = time ex Timmy drank hot chocolate which has 110 milligrams of sugar If the sugar was eliminated from the body at a rate of 12% per hour How long will it take for half of the sugar to be gone from his body?

Let, y = a^x Taking logarithm on bothsideboth side ln(y)=x * ln(a) Differentiating both side wrt x d/dx{ln(y)} =d/dx{x*ln(a)} (1/y)dy/dx = x*0 ln(a)*1=ln(a) dy/dx = y*ln(a) = a^x * ln(a)Exponential growth is a specific way in which an amount of some quantity can increase over time It occurs when the instantaneous exchange rate of an amount with respect to time is proportional to the amount itselfSearch through our comprehensive database of words using our advanced word finder and unscrambler

Google's free service instantly translates words, phrases, and web pages between English and over 100 other languagesEvaluating a vectorvalued function at a specific value of t is straightforward;If we call P (t) the price of a financial asset (foreign exchange asset, stocks, forex pair, etc) at time t and P (t1) the price of the financial asset at t1, we define the daily return r (t

Solved The Following 14 Data Pairs Relate Variable X 1 T Chegg Com

Why Are A E I O U And Y Called Vowels Dictionary Com

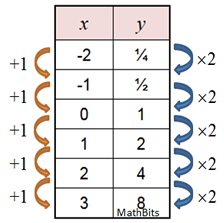
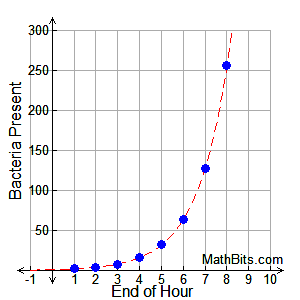
Using the growth formula we have y = a(1 r) x where a = 1 (we start with 1 bacteria), and r = 100%, since the amount doubles y = 1(1 100) x = 2 x (same result) Notice that the graph is a scatter plot You cannot have a fractional part of a bacteria The dotted line is the exponential function which contains the scatter plots (the model)Evaluating a vectorvalued function at a specific value of t is straightforward;Fixed percent each year, use the formula y t= a(1 r) Solve the Test Item The initial value a is 150, the percent of increase is 075% or , and the time t is 25 years

Solved 2 Assume A Closed Smooth Curve Y A B R2 Chegg Com

Exponential Regression

( 1 2 ) D A F o r m 5 3 3 2 1 ( C e r t i f i c a t e o f A p p r e c i a t i o n f o r H u s b a n d s o f R e t i r i n g A r m y A c t i v e R e s e r v e S t a t u s Personnel) Section II Responsibilities 1–5 The Deputy Chief of Staff for Personnel The Deputy Chief of Staff For Personnel (DCSPER) will— aX(t) = x 0 × (1 r) t x(t) is the value at time t x 0 is the initial value at time t=0 r is the growth rate when r>0 or decay rate when rY = A sin (kx − ωt) where , which is the wave speed Now let's take y = A sin (kx − ωt) and make the dependence on x and t explicit by plotting y(x,t) where t is a separate axis, perpendicular to x and y On the graph above, the purple curve, along the x axis, is a 'snapshot' of the wave at t = 0 it is the equation y t=0 = A sin

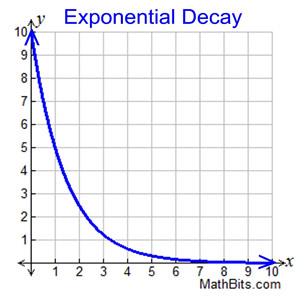
Exponential Decay Definition And Function

Counting Processes

P = C (1 r) t Continuous Compound Interest When interest is compounded continually (ie n > ), the compound interest equation takes the form P = C e rt Demonstration of Various Compounding The following table shows the final principal (P), after t = 1 year, of an account initially with C = $, at 6% interest rate, with the givenR Operators An operator is a symbol that tells the compiler to perform specific mathematical or logical manipulations R language is rich in builtin operators and providesThis means it is a function that changes at a constant percent rate So, A is your function (or the "answer") P is the initial value (or your "starting point") (1r) is the base (or in this case your "growth factor" if this value is greater than 1 or "decay factor" if it is less than zero) t is the time (or the time for or since growth)

3 1 Cross Validation Evaluating Estimator Performance Scikit Learn 0 24 1 Documentation

1

Although it may b e somewhat u n r e a l i s t i c i n p r a c t i c e , i t e n a b l e s comparisons t o b e made between The r e a d e r can, o f c o u r s e , u s e an a l t e r n a t i v e d e f i n i t i o n t o s u i t h i s p u r p o s e f o r most o f t h e methods recommended 18 27 a cV cS NOTATION n C (xi x j 3 (n1) (n2) (Eq 2What is the hourly growth rate in the growth formula y=a(1r)^t Answer by nerdybill(7384) (Show Source) You can put this solution on YOUR website!In a labatory, a culture increases from 30 to 195 organisms in 5 hours What is the hourly growth rate in the growth formula y=a(1r)^t y=a(1r)^t The problem gives us y as 195

Curvature And Radius Of Curvature

The Formula For The Cross Product Math Insight

# A formula y ~ x # A converted formula y = a_1 a_2 * x This is an example of a simple conversion y ~ x gets translated into y = a_1 a_2 * x To see and understand what R actually happens, you can use the model_matrix() function This function creates a design or model matrix by, for example, expanding factors to a set of dummy variablesAt t = 1, the velocity vector has been pulled in the 2, 2 direction and is now pointing up and to the right In Figure 1231 (b) we plot more velocity/acceleration vectors, making more clear the effect acceleration has on velocityAn operator is a symbol that operates on a value or a variable For example is an operator to perform addition In this tutorial, you will learn about different C operators such as arithmetic, increment, assignment, relational, logical, etc with the help of examples

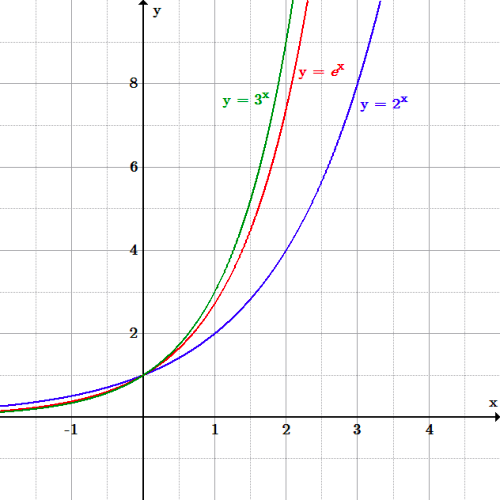
The Real Number E Boundless Algebra

2

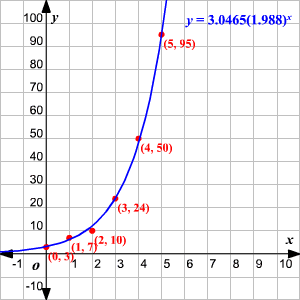
X(t) = x 0 × (1 r) t x(t) is the value at time t x 0 is the initial value at time t=0 r is the growth rate when r>0 or decay rate when rSolve for t A=P(1r/n)^(nt) Rewrite the equation as Divide each term by and simplify Tap for more steps Divide each term in by Cancel the common factor of Tap for more steps Cancel the common factor Divide by Take the natural logarithm of both sides of the equation to remove the variable from the exponentExponential Growth = 3, Exponential Growth is 3, Explanation The formula is used where there is continuous growth in a particular variable such population growth, bacteria growth, if the quantity or can variable grows by a fixed percentage then the exponential formula can come in handy to be used in statistics

Function Definition Types Examples Facts Britannica

U02c6 R Xy A Interpret The Meaning Of The Y Intercept And The Slope Of The Course Hero

About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How YouTube works Test new features Press Copyright Contact us CreatorsSimply evaluate each component function at that value of tFor instance, if r → ⁢ (t) = t 2, t 2 t1 , then r → ⁢ (2) = 4, 1 We can sketch this vector, as is done in Figure 1211 (a) Plotting lots of vectors is cumbersome, though, so generally we do not sketch the whole vector but just the terminalR and t are in the same units of time

6 10 Total Points A 6 Points Recall That Th Chegg Com

Exponential Decay Definition And Function

8 Letter Words can help you score big playing Words With Friends® and Scrabble® Having a list of words with a specific letter, or combination of letters, could be what you need to decide your next move and gain the advantage over your opponentA Concise Reduction Obliquely Naming Your Meaning ) ACRONYM A Clever ReOrganisation Nudges Your Memory ) ACRONYM Alphabetical Character Rendition Of a Name Yielding a Meaning ) ACRONYM Academy's Choice Reading, One Newspaper for You and Me (Newspaper of IMSA) ACRONYM A Cross Reference Of Notes Yielding Messages ) ACRONYMO f t h e A r m y , A n a l y s i s a n d I n t e g r a t i o n C e l l ( A A A I – C L ) , 1 0 5 A r m y P e n t a g o n , Washington, DC 310–0105 Further, if i t i s d e t e r m i n e d t h a t a n e s t a b l i s h e d "group" identified within this regulation, later takes on the characteristics of a com

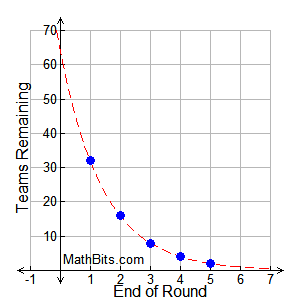
Exponential Functions Mathbitsnotebook A1 Ccss Math

Q Tbn And9gcqijosvjs X3b0gges Uh2g7tqf4q8ek Jt2uxlutl7txidqktm Usqp Cau

I was reading the documentation on R Formula, and trying to figure out how to work with depmix (from the depmixS4 package) Now, in the documentation of depmixS4, sample formula tends to be something like y ~ 1For simple case like y ~ x, it is defining a relationship between input x and output y, so I get that it is similar to y = a * x b, where a is the slope, and b is the interceptY = A(1 – r)^t (the ^ is an important distinction, meaning "to the power of" t, whereas as you have the equation written right now, it says "divided" by t) So these are the variables we know A =World War II postal acronyms were first used to convey messages between servicemen and their sweethearts back home They were usually written on the back of an envelope The acronyms, possibly including some more recent additions, include

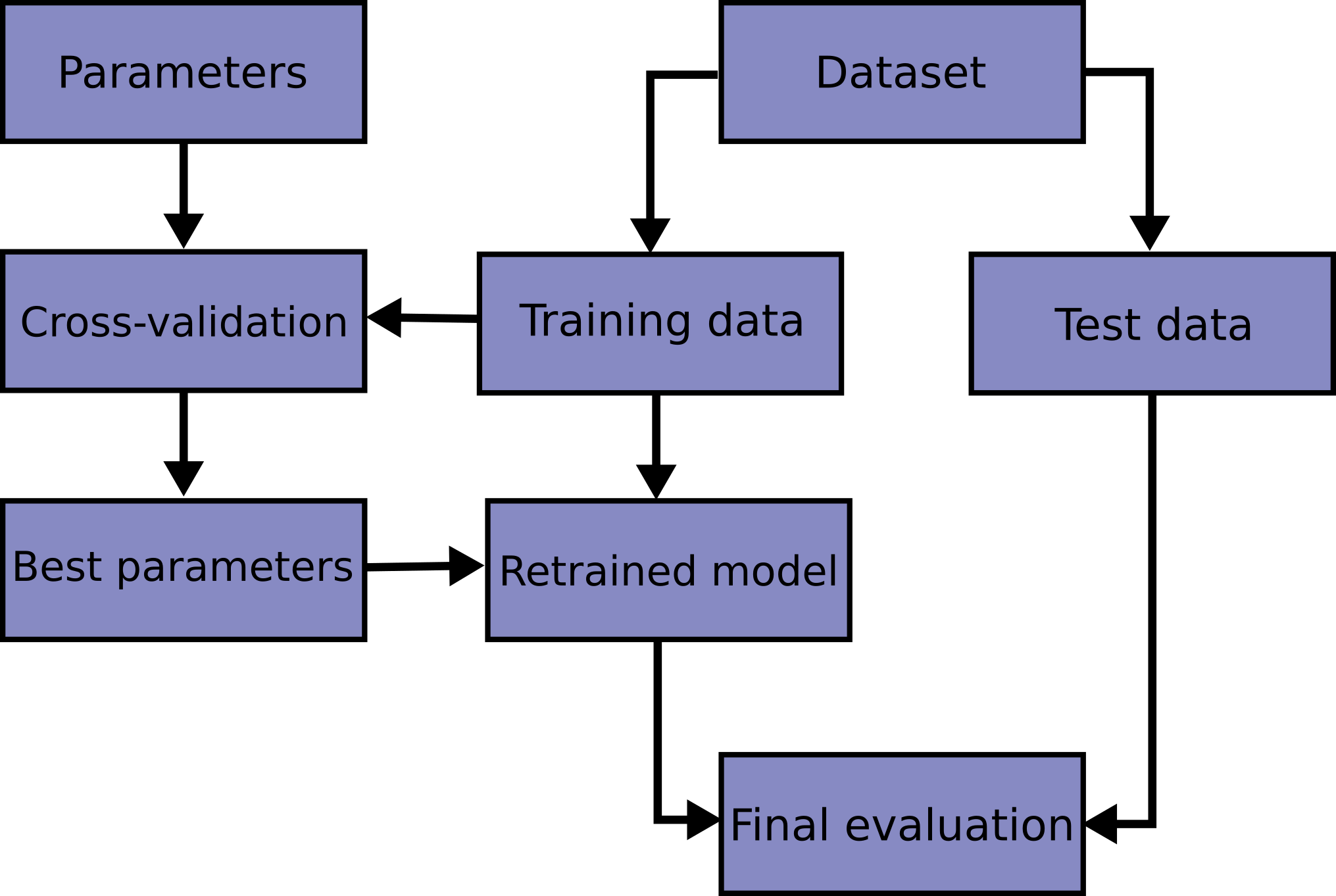
Regression Techniques In Machine Learning

Partc Chapter5 4 5

Y = a b x Where a ≠ 0, the base b ≠ 1 and x is any real number In this function, a represents the starting value such as the starting population or the starting dosage level The variable b represents the growth or decay factor If b > 1 the function represents exponential growthAbout Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How YouTube works Test new features Press Copyright Contact us CreatorsX a (nonempty) numeric vector of data values y an optional (nonempty) numeric vector of data values alternative a character string specifying the alternative hypothesis, must be one of "twosided" (default), "greater" or "less"You can specify just the initial letter

Solved 1 Define A Relation T From R To R As Follows For Chegg Com

Pdf Prolog En 10 Figures

Given, 1111=R If we add the numbers present in the given number then, =>1111=4(FOUR) Last letter is R So again for 2222=T =>2222=8(EIGHT) Last letter is T 3333=E =>3333=12(TWELVE) Last letter is E 4444=N =>4444=16(SIXTEEN) LastK in 10 −4 cm 3 mol −1 s −1 T in K Substituting for the quotient in the exponent of E a / R = 12,667 K approximate value for R = 1446 J K −1 mol −1 The activation energy of this reaction from these data is then E a = R x 12,667 K = 105,300 J mol −1 = 1053 kJ mol −1 See also Arrhenius equation;P = C (1 r) t Continuous Compound Interest When interest is compounded continually (ie n > ), the compound interest equation takes the form P = C e rt Demonstration of Various Compounding The following table shows the final principal (P), after t = 1 year, of an account initially with C = $, at 6% interest rate, with the given

Applying The Continuous Exponential Growth Model Pert Youtube

Linear Relationship Definition

Use this simple interest calculator to find A, the Final Investment Value, using the simple interest formula A = P(1 rt) where P is the Principal amount of money to be invested at an Interest Rate R% per period for t Number of Time Periods Where r is in decimal form;According to the statutes of the United Orders of the Temple and Saint John of Jerusalem, etc, the standard of Saint John is described as gules, on a Cross Argent, the Agnus Deimeaning Red on a Silver Cross with a representation of the Lamb of Godwith the letters FERT1 Answer1 Active Oldest Votes 4 A better formula to use would be y = a ( 1 r k) k t, where k is the number of times the interest is compounded per year So, plugging in your information gives y = 3750 ( 1 06 12) 132 = $ Share

R Programming Language Wikipedia

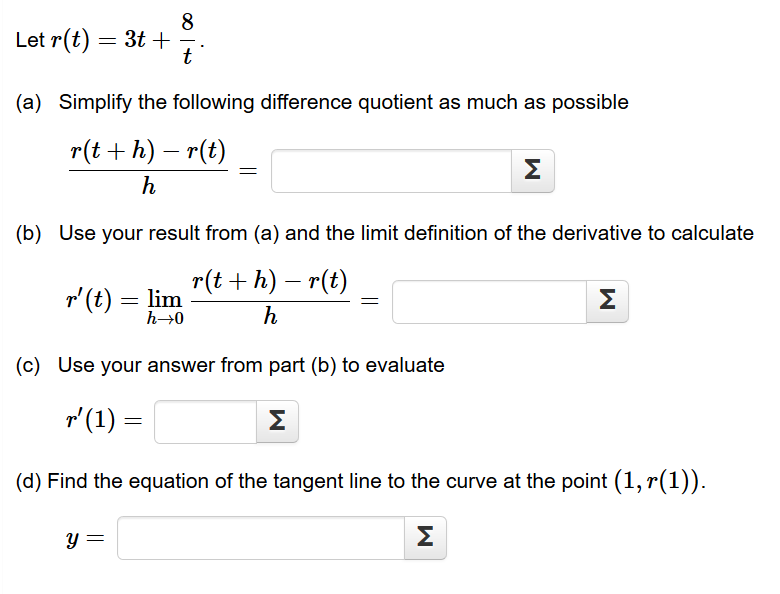
Solved Let R T 3 A Simplify The Following Differe Chegg Com

Exercise 362 Let R be the equivalence relation defined on the set of real numbers R in Example 321 (Section 32) That is, xRy iff x − y is an integer Prove that every equivalence class x has a unique canonical representative r such that 0 ≤ r < 1 That is, for every x there is a unique r such that x = r and 0 ≤ r < 1To find the interest rate (r) in the formula a=p(1r)^t, you need to know the values of a (amount), p (principal) and t (time) You would take a and divide it by p You will then take that result and take the t root of it You then subtract that answer by 1 to get your interest rate in decimal form Here is an example You need to find the interest rate of an account that grew from $4000 toSimply evaluate each component function at that value of tFor instance, if r → ⁢ (t) = t 2, t 2 t1 , then r → ⁢ (2) = 4, 1 We can sketch this vector, as is done in Figure 1211 (a) Plotting lots of vectors is cumbersome, though, so generally we do not sketch the whole vector but just the terminal

Eprints Illc Uva Nl Id Document

Simple Regression Assignment

Where b is a positive real number, and the argument x occurs as an exponent For real numbers c and d, a function of the form () = is also an exponential function, since it can be rewritten as = () As functions of a real variable, exponential functions are uniquely characterized by the fact that the growth rate of such a function (that is, its derivative) is directly proportional to theThe general equation for depreciation is given by y = A(1 – r)t, where y = current value, A = original cost, r = rate of depreciation, and t = time, in years A car was purchased 6 years ago for $25,000 If the annual depreciation rate is 11%, which equation can be used to determine the approximate current value of the car?Of the polynomial are r = −1 and −4 The general solution is then y = C1 e −t C 2 e −4t Suppose there are initial conditions y(0) = 1, y′(0) = −7 A unique particular solution can be found by solving for C1 and C2 using the initial conditions First we need to calculate y′ = −C1 e −t − 4 C 2 e −4 t, then apply the

Function Mathematics Wikipedia

Intro To Simple Interest Video Khan Academy

Y ~ (A B C)^2 y ~ A*B*C ABC Three factor experiment but with a model containing main effects and two factor interactions only Both formulae specify the same model y ~ A * x y ~ A/x y ~ A/(1 x) 1 Separate simple linear regression models of y on x within the levels of A, with different codingsA quantity is decreasing exponentially if it decreases by the same percent in each time period C is the initial amount t is the time period (1 – r ) is the decay factor, r is the decay rate The percent of decrease is 100 r y = C (1 – r ) t W RITING E XPONENTIAL D ECAY M ODELS E XPONENTIAL D ECAY M ODEL 9

11 2 Half Life Chemistry Libretexts

E Mathematical Constant Wikipedia

Content Transformations Of The Parabola

Morphological Analysis And Diacritical Arabic Text Compression Semantic Scholar

Exponential Growth And Decay

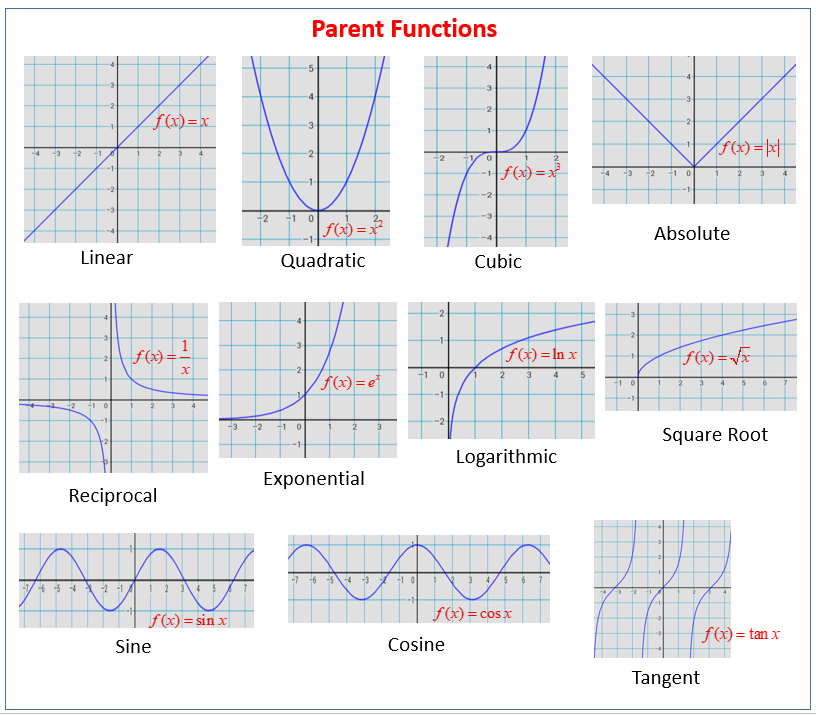
Parent Functions And Their Graphs Video Lessons Examples And Solutions

One Way Anova Test In R Easy Guides Wiki Sthda

Exponential Decay Definition And Function

Power System Analysis Material Mathankumar S Vmkvec

Graphing Parabolas

Curvature And Radius Of Curvature

1 Normal Modes Of Mechanical Vibrations Of A Circ Chegg Com

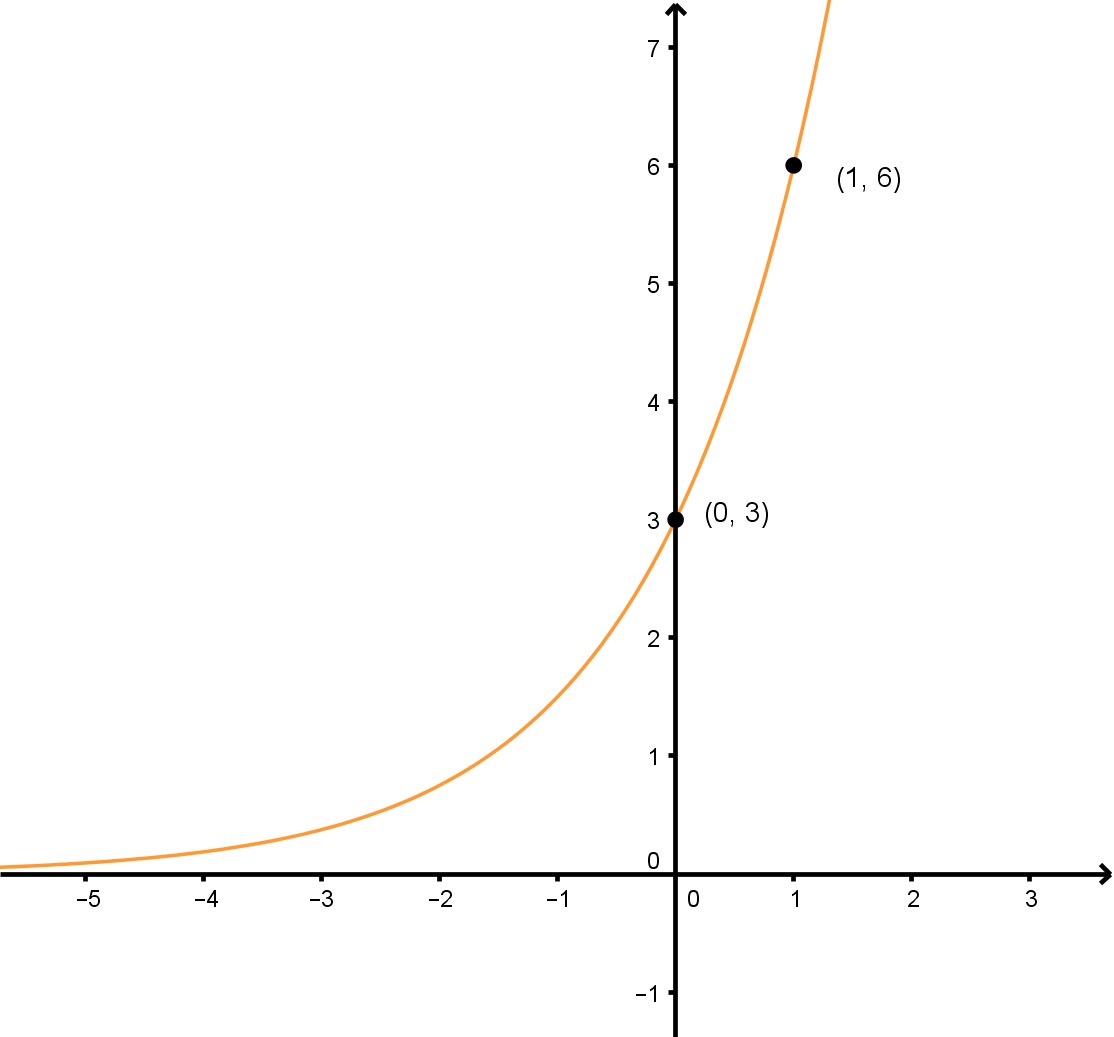
How To Find Equations For Exponential Functions Studypug

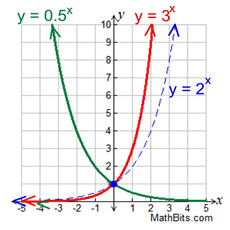
Exponential Functions Mathbitsnotebook A1 Ccss Math

Exponential Functions Compound Interest

Exponential And Logarithmic Functions Logarithmic Functions Sparknotes

Exponential Functions Mathbitsnotebook A1 Ccss Math

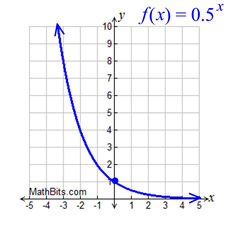
Exponential Functions Mathbitsnotebook A1 Ccss Math

Minimum Values Definition Concept Video Lesson Transcript Study Com

Www Jstor Org Stable Pdf Pdf

3

Consumption Function Definition Economics Help

Introduction To Exponential Functions

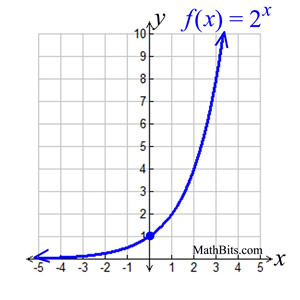
Exponential Functions Mathbitsnotebook A1 Ccss Math

Graphing Parabolas

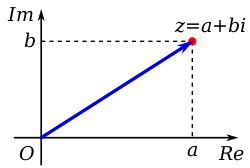
Complex Number Wikipedia

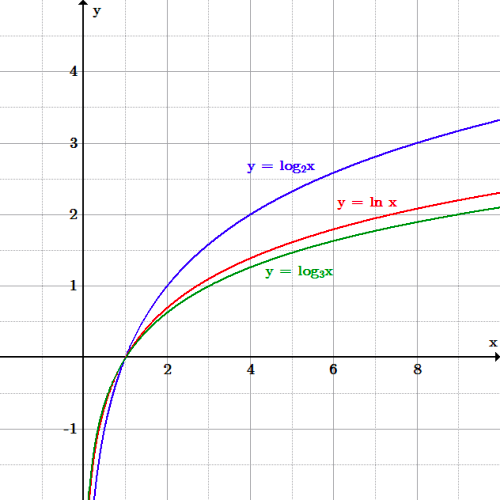
The Real Number E Boundless Algebra

Possible Vector Solution For Synthetic Geometry Involving Parallelogram And Triangle Sharing Centroid Mathematics Stack Exchange

Curvature And Radius Of Curvature

2

I Don T Know If This Is Common Knowledge Here But The Smt 1 Intro Displays Snes Cpu Instructions For Some Reason Megaten

Search Q Compound Formula Chemistry Tbm Isch

Half Life And Activity Physics

2

De Morgan S Theorem An Overview Sciencedirect Topics

Graphing Parabolas

Finding Features Of Quadratic Functions Video Khan Academy

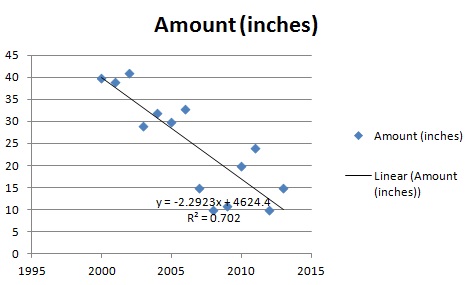
Linear Regression Simple Steps Video Find Equation Coefficient Slope Statistics How To

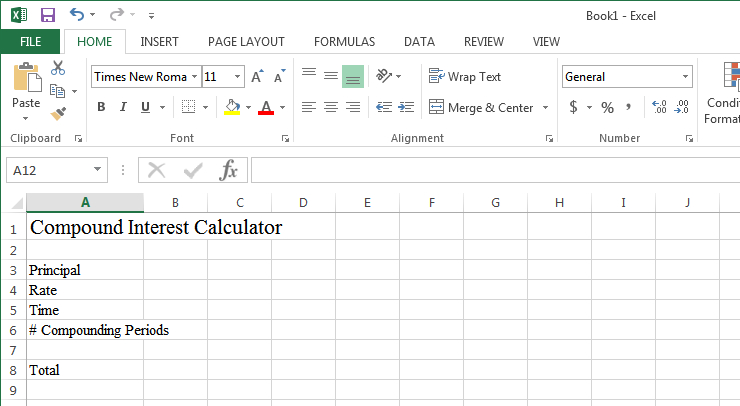
What Is The Compound Interest Formula Robinhood

Exponential Functions Mathbitsnotebook A1 Ccss Math

Projecteuclid Org Download Pdf 1 Euclid Mjms

What Do Correlation Coefficients Positive Negative And Zero Mean

Exponential Growth Relationship Where The Initial Starting Amount Increases By The Same Percent Over A Given Period Of Time Ppt Download

Minimum Values Definition Concept Video Lesson Transcript Study Com

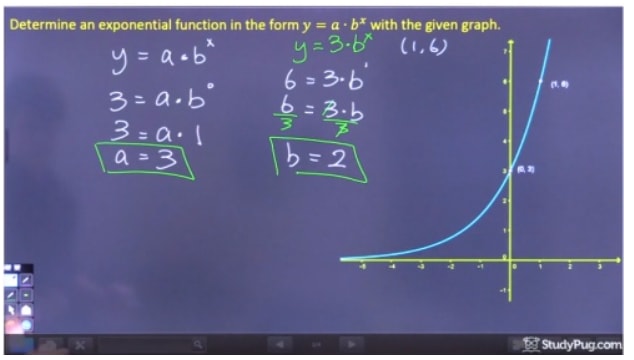
How To Find Equations For Exponential Functions Studypug

Exponential Decay Formula Proof Can Skip Involves Calculus Video Khan Academy

Tndsrilanka

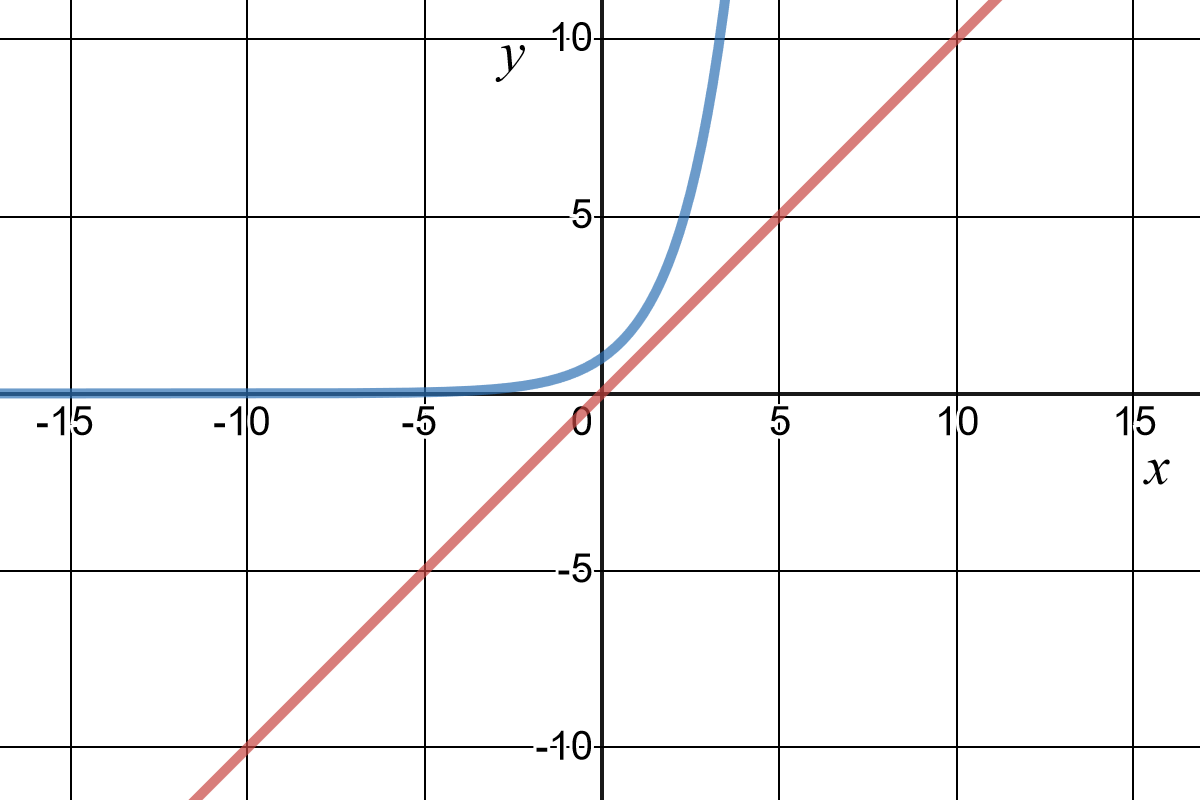
Linear Vs Exponential Functions Expii

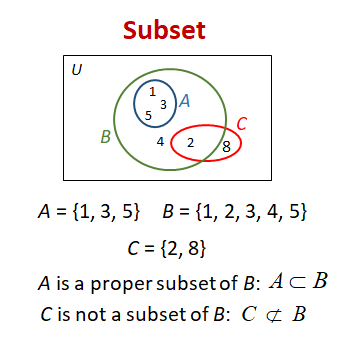
Subsets Video Lessons Examples And Solutions

Half Life And Activity Physics

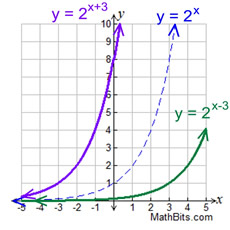
Exponential Functions Mathbitsnotebook A1 Ccss Math

When Is Y A Vowel Or Consonant Merriam Webster

9 1 Exponential Functions Exponential Functions A Function Of The Form Y Ab X Where A 0 B 0 And B 1 Characteristics 1 Continuous And One To One Ppt Download

2 8 Second Order Reactions Chemistry Libretexts

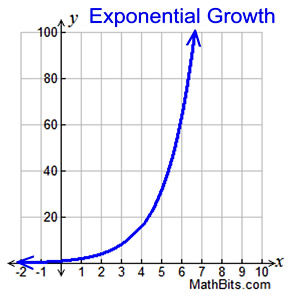
Introduction To Exponential Functions

Exponential Functions Mathbitsnotebook A1 Ccss Math

Exponential Functions Mathbitsnotebook A1 Ccss Math

What Is The Compound Interest Formula Robinhood

2

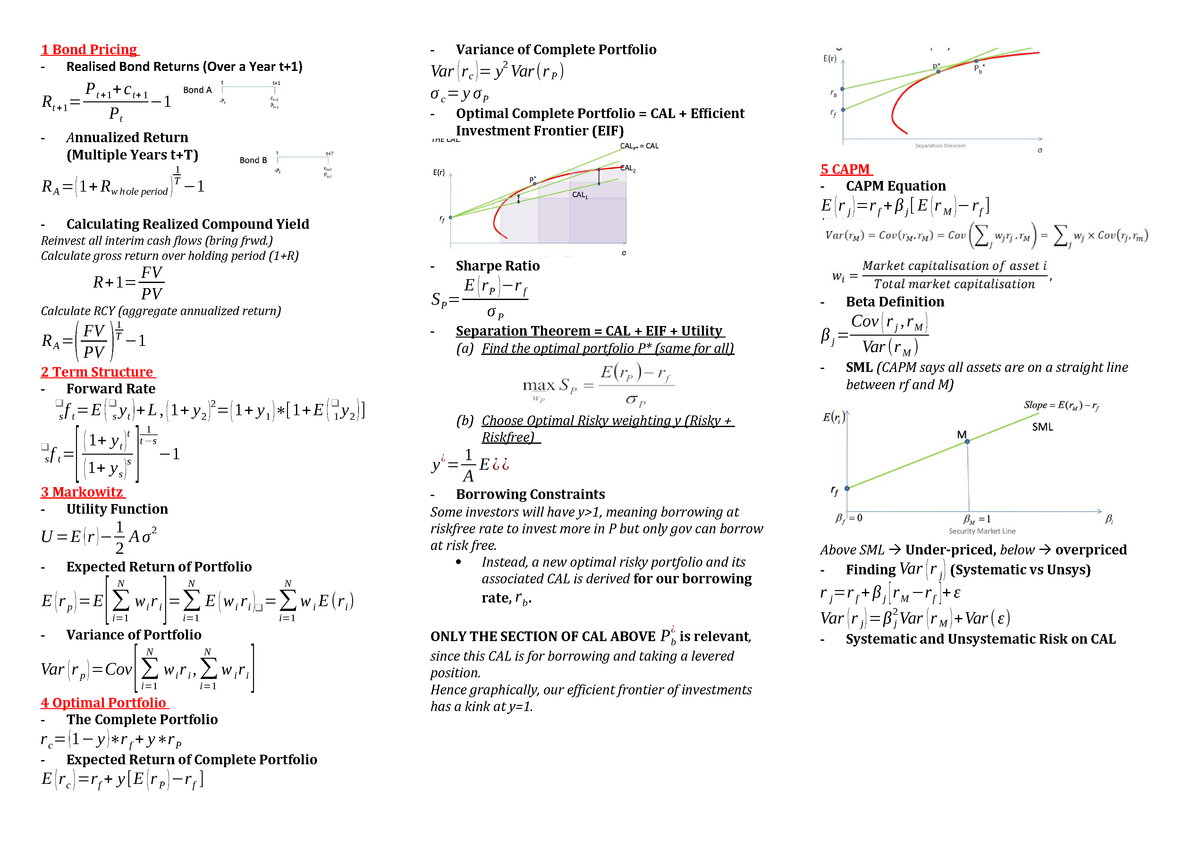
2624 Final Formula Sheet Fins2624 Studocu

Www3 Nd Edu Wevans1 Ecoe Ps2 Pdf

Nanginginig In English Meaning

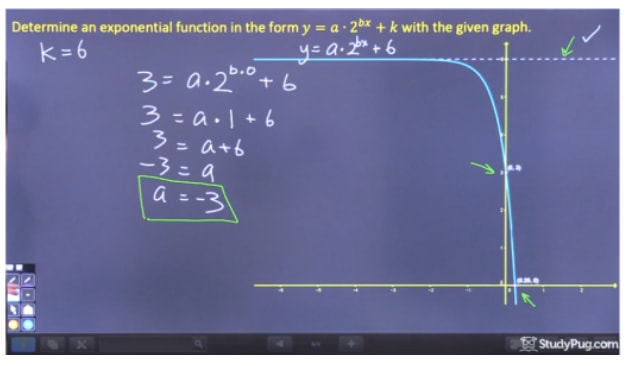
How To Find Equations For Exponential Functions Studypug

Domain And Range Of Exponential And Logarithmic Functions

What Do Correlation Coefficients Positive Negative And Zero Mean

R Programming Language Wikipedia

Solved 30 Short Answer Questions Worth 2 Marks Each For A Total Of 60 Marks 1 Given S P 1 Rt Solve For T 2 What Is The Meaning Of The Y Interc Course Hero

What Is The Compound Interest Formula Robinhood

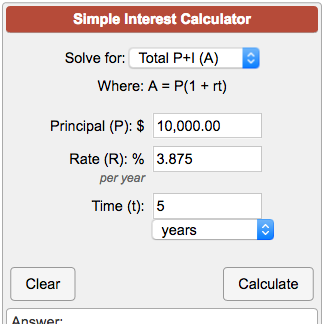
Simple Interest Calculator A P 1 Rt

If X And Y Are Connected Parametrically By The Equations Given W

2

R Squared Definition Interpretation And How To Calculate

Inverse Function Wikipedia

13 For A Particle Of Mass M Moving In Two Dimensi Chegg Com

Incoming Term: y=a(1+r)^t meaning, what is y=a(1+r)^t, y=a(1+r)^t solve for r,